为解决机床柔性主轴转子动平衡过程中需要在高速下试重的问题,提出一种柔性主轴转子低速无试重动平衡方法。在构建机床主轴动力学模型的基础上,根据刚体力学理论,通过对不平衡量与振动响应之间映射关系的提取,实现了工作转速下采集一次振动数据即可完成不平衡量的无试重识别。

为了在非真实失衡面对呈现柔性特征的主轴转子失衡振动进行有效抑制,分析了柔性状态下的不平衡主轴模态振动行为,并基于此提出了不平衡量校正位置迁移方法。在高速柔性电主轴动平衡平台上进行了仿真与实验分析,实验在7200r/min时进行,结果表明:基于一阶临界转速下所采集的振动数据,可得到迁移至两侧配重平面的等效不平衡量,对该不平衡量予以校正之后,一阶临界转速下主轴振动幅值下74.7,且临界转速前后的振动降幅也较为明显,有效抑制了高速振型不平衡。
装备制造行业正朝着高速、高精度方向发展,这需要精准的数字装备予以支撑。数控机床是数字装备最高技术水平的载体之一,主轴系统作为现代数控机床的关键部件,其动态特性直接制约着零件制造精度。由于装配工艺、变工况以及磨损等因素,主轴通常处于不平衡状态。机床主轴作速度较高,不平衡引起的主轴振动尤为明显,这直接影响加工质量,甚至导致主轴组件损坏。因此,必须采取措施控制主轴不平衡振动。针对这一问题,国内外开展了动平衡方法的研究。动平衡是典型的已知输出求解输入的逆问题,工程中通常进行多次启停车以添加试重,从而获取转子影响系数、敏感因子等特性响应参数。然而,试重意味着自动化环节的中断,破坏了高效加工的原则,并且错误的试重更会使高速主轴运转状态急剧恶化。能否通过最少的试重次数实现转子的高效、平稳运行,是衡量现场动平衡方法的一个重要指标。如果试重选择得当,可以实现“试重即配重”的效果,能实现这一效果的方法被称为“无试重平衡方法”。
大多数无试重平衡方法通常需要在临界转速或靠近l临界转速时多次获取转子振动信息,这增加了动平衡实施过程中的复杂性和风险性,也容易降低主轴系统的使用寿命。为克服上述问题,本文结合刚体力学平衡理论,提出一种仅需在低于临界转速下对主轴采集一次振动数据,即可无试重识别主轴不平衡量的策略,进而研究了基于模态分析方法的不平衡量校正位置迁移方法,实现了在低速下对柔性主轴不平衡振动的有效抑制。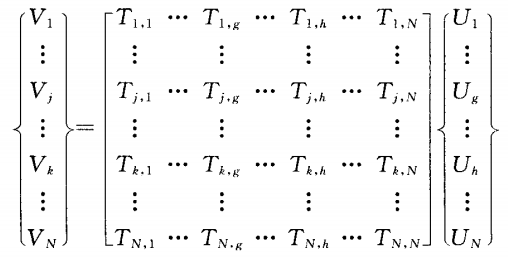
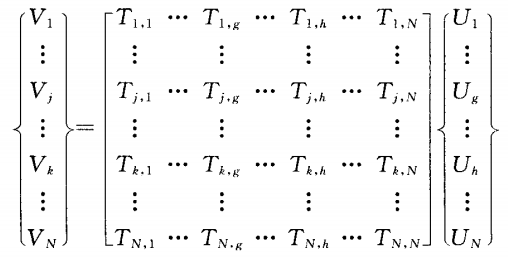
不平衡量无试重求解有限元方法在转子动力学分析中得到了广泛应用,主轴有限元模型通常由离散质量圆盘、连续质量轴段以及弹性轴承座等单元组成,综合各单元运动微分方程,可得主轴系统运动方程为一ioJz,+KZ—n。Ue(1)式中:z为系统位移向量;为自转角速度;M为质量矩阵;I,为陀螺矩阵;K为刚度矩阵;U为不平衡矢量,对于具有N个结点的主轴系统U一{m1£leiel,m2e2e2,…,N£NeiN)T(2)其中e为偏心距,为u在单元截面的方位角。设不平衡响应的特解为Z—Ve(3)代入式(1)得振动响应向量V—nr~M+t,+K1lU(4)若u为已知,通过式(4)可求解V。
主轴在装配之前,轴体本身的不平衡量在平衡机上经过离线动平衡后,残余不平衡量很小。然而,在主轴运转时,不平衡量仍不可忽视,且更多出现在电机绕组及刀具刀柄处。这主要是因为电机绕组结构较为复杂,高速下离心膨胀现象更为突出,其动平衡精度难以保证,而刀具在加工过程中频繁使用和更换,无论是刀具磨损还是刀具更换时的安装偏心都容易导致新的不平衡。假设在主轴前后端轴承位置设置振动监测点,相应结点编号分别为J、是,刀具及电机绕组两处结点编号分别为g、h。
407 浏览





